问题
解答题
已知等差数列{an}的前n项和为Sn，且a6=﹣5，S4=﹣62．
（1）求{an}通项公式；
（2）求数列{|an|}的前n项和Tn．
答案
解：（1）设等差数列{an}的公差为d，则
由条件得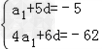
，
解得
，
所以{an}通项公式an=﹣20+3（n﹣1），则an=3n﹣23
（2）令3n﹣23≥0，则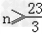
，所以，当n≤7时，an＜0，当n≥8时，an＞0．
所以，当n≤7时，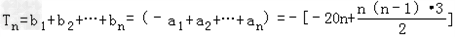
=
，
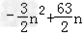当n≥8时，Tn=b1+b2+…+bn=﹣（a1+a2+…+a7）+a8+…+an
=﹣2（a1+a2+…+a7）+a1+a2+…+a7+a8+…+an
=
，
．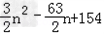
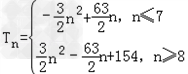