问题
填空题
已知在△ABC中，∠ACB=90°,∠A=30°，BC=2cm，CD⊥AB于点D，则AD=
答案
3
解：如图，
 |
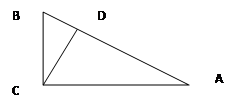在Rt△ABC中，∠ACB=90°,∠A=30°，BC=2cm，所以斜边AB=4cm
又因为CD⊥AB于点D，所以∠BCD=∠A=30°.
所以在Rt△BCD中， BD=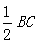
=1cm
所以AD=AB-BD=4-1=3
故答案为3cm
搜题请搜索小程序“爱下问搜题”
已知在△ABC中，∠ACB=90°,∠A=30°，BC=2cm，CD⊥AB于点D，则AD=
3
解：如图，
|
在Rt△ABC中，∠ACB=90°,∠A=30°，BC=2cm，所以斜边AB=4cm
又因为CD⊥AB于点D，所以∠BCD=∠A=30°.
所以在Rt△BCD中， BD=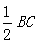=1cm
所以AD=AB-BD=4-1=3
故答案为3cm