问题
证明题
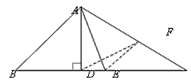
△ABC中,AB<AC,AD、AE分别是BC边上的高和中线,且∠BAD=∠EAC,证明∠BAC是直角。
答案
证明:如图,取AC的中点F,连结EF、DF,
EF为三角形△ABC的中位线,故有EF∥AB,∠AEF=∠EAB, ①
又由∠BAD=∠EAC,所以∠EAB=∠DAC, ②
因AD是BC边上的高,则△ADC是直角三角形,则DF=AF,
于是∠ADF=∠DAC, ③
联合①、②,得∠ADF=∠AEF,
由此,得A、D、E、F四点共圆,
于是,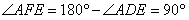 ,
,
因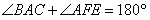 ,故∠BAC=90°。
,故∠BAC=90°。