问题
证明题
⊙O内切于△ABC的边于D,E,F,AB=AC,连接AD交⊙O于点H,直线HF交BC的延长线于点G。
(1)求证:圆心O在直线AD上;
(2)求证:点C是线段GD的中点。
答案
解:(1 )∵
∴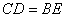
又∵
∴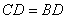
又∵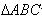 是等腰三角形
是等腰三角形
∴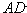 是
是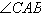 的角分线
的角分线
∴圆心O在直线AD上。
(2)连接DF,由(1)知,DH是⊙O的直径,
∴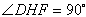
∴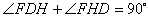
又∵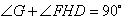
∴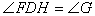
∵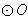 与AC相切于点F
与AC相切于点F
所以
∴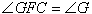
∴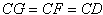
∴点C是线段GD的中点。
⊙O内切于△ABC的边于D,E,F,AB=AC,连接AD交⊙O于点H,直线HF交BC的延长线于点G。
(1)求证:圆心O在直线AD上;
(2)求证:点C是线段GD的中点。
解:(1 )∵
∴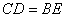
又∵
∴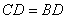
又∵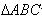 是等腰三角形
是等腰三角形
∴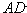 是
是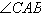 的角分线
的角分线
∴圆心O在直线AD上。
(2)连接DF,由(1)知,DH是⊙O的直径,
∴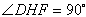
∴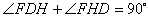
又∵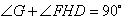
∴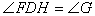
∵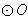 与AC相切于点F
与AC相切于点F
所以
∴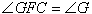
∴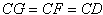
∴点C是线段GD的中点。