问题
选择题
若函数f(x)=kx-|x|+|x-2|有3个零点,实数k的取值范围是( )
A.[1,+∞)
B.(0,1]
C.(1,+∞)
D.(0,1)
答案
答案:D
解:构建函数f1(x)=kx,f2(x)=|x|-|x-2|,则函数f(x)=kx-|x|+|x-2|有3个零点时,两个函数的图象有3个交点
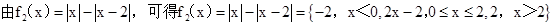
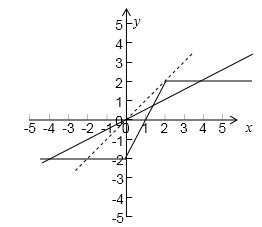
作出函数的图象,可知k∈(0,1)时,两个函数的图象有3个交点
故选D.
若函数f(x)=kx-|x|+|x-2|有3个零点,实数k的取值范围是( )
A.[1,+∞)
B.(0,1]
C.(1,+∞)
D.(0,1)
答案:D
解:构建函数f1(x)=kx,f2(x)=|x|-|x-2|,则函数f(x)=kx-|x|+|x-2|有3个零点时,两个函数的图象有3个交点
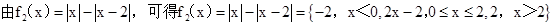

作出函数的图象,可知k∈(0,1)时,两个函数的图象有3个交点
故选D.