问题
解答题
已知关于x的方程ax2+2x+1=0至少有一负根,求a的取值范围.
答案
解:(1)当a=0时,方程变为2x+1=0,有一负根x=﹣ ,满足题意
,满足题意
(2)当a<0时,△=4﹣4a>0,方程的两根满足
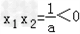 ,
,
此时有且仅有一个负根,满足题意(3)
当a>0时,由方程的根与系数关系可得,
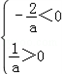
∴方程若有根,则两根都为负根,
而方程有根的条件△=4﹣4a≥0
∴0<a≤1
综上可得,a≤1
已知关于x的方程ax2+2x+1=0至少有一负根,求a的取值范围.
解:(1)当a=0时,方程变为2x+1=0,有一负根x=﹣ ,满足题意
,满足题意
(2)当a<0时,△=4﹣4a>0,方程的两根满足
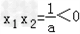 ,
,
此时有且仅有一个负根,满足题意(3)
当a>0时,由方程的根与系数关系可得,
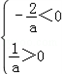
∴方程若有根,则两根都为负根,
而方程有根的条件△=4﹣4a≥0
∴0<a≤1
综上可得,a≤1