问题
选择题
在Rt△ACB中,∠C=90°,∠A=30°,在直线BC或直线AC上找到一点P,使△PAB是等腰三角形,则满足条件的点P的个数是
A.4
B.6
C.7
D.8
答案
答案:B
分析:根据题意,点P在直线BC或直线AC上,使△PAB是等腰三角形,则三角形的两底角相等,两腰相等.
解答:解:如图:
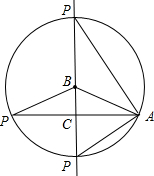
当以B为圆心,AB长为半径作圆,交直线BC于两点,即为P,交直线AC于一点,此题符合条件的P点有3个;
同理:当以A为圆心,AB长为半径作圆,交直线AC于两点,即为P,交直线BC于一点,此题符合条件的P点有2个;
作AB的垂直平分线交AC于点P,交BC的延长线于P,此题符合条件的P点有2个,AB的垂直平分线和BC直线的交点与之前的交点重合.
故有6个点.
故选B
