如图所示的传送带,其水平部分AB长SAB=3.2m,BC部分与水平面夹角θ为37°,长度SBC=22m,一小物体P与传送带的动摩擦因数µ=0.25,皮带沿A至B方向运行,速率恒为v=12m/s,若把物体P无初速度的放在A点处,它将被传送带送到C点(B处为一小曲面,不改变速度的大小,只改变速度的方向),且物体P不脱离传送带.求
(1)物体到达B点的速度;
(2)物体刚进入传送带BC部分的加速度;
(3)物体从A点运动到C点所用的时间?
(g=10m/s2,sin37°=0.6,cos37°=0.8)
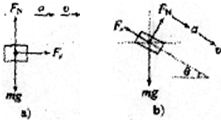
(1)物体放于传送带上A点后,物块受力图如答图a所示.先在传送带上做匀加速运动(相对地面),直到与传送带速度相同为止,此过程物体的加速度为a1,则有:μmg=ma1,a1=μg=2.5m/s2
做匀加速运动的时间是:t1=
=v a1
s=4.8s12 2.5
这段时间内物体对地的位移是s1=
•t1=v 2
×4.8m=28.8m12 2
∵s1=28.8m>SAB=3.2m
∴从A到B物体一直做匀加速运动,设达到B点的速度为vB,则
=2a1SABv 2B
代入解得:vB=4m/s,所用时间为t1=
=vB a1
s=1.6s4 2.5
(2)物块在传送带的BC之间,受力情况如图b
,
由于μ=0.25<tan37°=0.75,A在BC段将沿倾斜部分加速下滑,此时A受到的为滑动摩擦力,大小为 μmgcos37°,方向沿传送带向上,
由牛顿第二定律:mgsin37°-μmgcos37°=ma2
a2=g(sin37°-μcos37°)=4m/s2
(3)物体在传送带的倾斜BC部分,以加速度a2向下匀加速运动,
由运动学公式SBC=vBt2+
a21 2 t 22
其中SBC=22m,vB=4m/s
解得t2=2
-1≈2.46s,3
物块从a到c端所用时间为t=t1+t2=4.06s
答:
(1)物体到达B点的速度是4m/s;
(2)物体刚进入传送带BC部分的加速度是4m/s2;
(3)物体从A点运动到C点所用的时间是4.06s.
