答案：D

在△ABC中，根据第三边的范围应大于已知两边的差，小于两边的和，得2＜AC＜6．在△ACD中，根据三角形的三边关系进行求解．

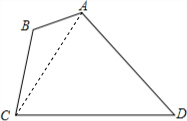
解：连接AC．

∵AB=2，BC=4，

在△ABC中，根据三角形的三边关系，4-2＜AC＜2+4，即2＜AC＜6．

∴-6＜-AC＜-2，1＜CD-AC＜5，9＜CD+AC＜13，

在△ACD中，根据三角形的三边关系，得CD-AC＜AD＜CD+AC，

∴1＜AD＜13．

故AD的取值范围是1＜AD＜13．

本题综合考查了三角形的三边关系．连接AC，求出AC的取值范围是解题关键．