问题
解答题
在直角三角形中，∠ACB=90°，CD是AB边上的高，AB=10cm，BC=8cm，AC=6cm.
（1）△ABC的面积；
（2）求CD的长？
（3）若△ABC的边AC上的中线是BE，求△ABE的面积.
答案
（1）S△ABC=24 （2）BC=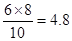
（3）S△ABE=
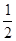S△ABC=12
分析：（1）先画图，根据直角三角形面积的求法，即可得出△ABC的面积；
（2）根据三角形的面积公式即可求得CD的长；
（3）根据中线的性质可得出△ABE和△BCE的面积相等，从而得出答案．
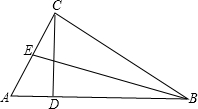解：（1）∵∠ACB=90°，BC=8cm，AC=6cm，
∴S△ABC=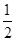
AC?BC=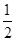×6×8=24；
（2）∵S△ABC=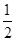×AB×CD=24，
∴CD=4.8cm；
（3）∵AE=CE，
∴S△ABE=S△BCE=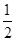S△ABC=12，
∴△ABE的面积为12cm2．