问题
单项选择题
线性齐次方程组(Ⅰ):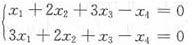
与线性齐次方程组(Ⅱ):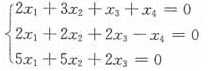
的全部公共解是()。
A.k1[1,-2,1,0]T+k2[0,1,0,2]T(k1,k2为任意数)
B.k[1,-2,1,0]T(k为任意数)
C.k[0,1,0,2]T(k为任意数)
D.k[5,-7,5,6]T(k为任意数)
答案
参考答案:D
解析:
解法1:把(Ⅱ)与(Ⅱ)联立得方程组(Ⅲ),方程组(Ⅲ)的全部解就是所需要的(Ⅰ)与(Ⅱ)的全部公共解,方程组(Ⅲ)的系数矩阵为
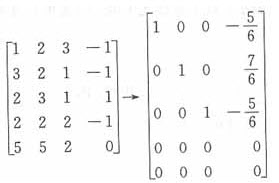
方程组(Ⅲ)的解为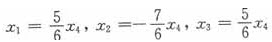
方程组(Ⅲ)的基础解系为
α=[5,-7,5,6]T
方程组(Ⅲ)的全部解为
k[5,-7,5,6]T,k为任意数
解法2:先求方程组(Ⅰ)的全部解,方程组(Ⅰ)的系数矩阵为

方程组(Ⅰ)的解为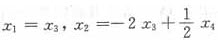
方程组(Ⅰ)的基础解系为
α1=[1,-2,1,0]T,α2=[0,1,0,2]T
方程组(Ⅰ)的全部解为
k1[1,-2,1,0]T+k2[0,1,0,2]T=[k1,-2k1+k2,k1,2k2]T
将方程组(Ⅰ)的全部解代入方程(Ⅱ)得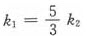
将它代入方程组(Ⅰ)的全部解得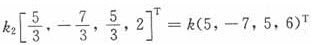
其中k为任意数,它就是(Ⅰ)与(Ⅱ)的全部公共解,故正确答案为D。
