解：（1）证明：①函数f（x）=a^x（n>1）具有性质P

f（x-1）+f（x+1）-2f（x）=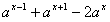

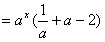
因为a>1，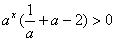

即f（x-1）+f（x+1）≥2f（x），此函数为具有性质P；

②函数f（x）=x³不具有性质P

例如，当x=-1时，f（x-1）+f（x+1）=f（-2）+f（0）=-8，

2f（x）=-2，

所以，f（-2）+f（0）＜f（-1），此函数不具有性质P。

（2）假设f（i）为f（1），f（2），…，f（n-1）中第一个大于0的值，

则f（1）- f（i-1）>0，

因为函数f（x）具有性质P，所以，对于任意n∈N*，

均有f（n+1）-f（n）≥f（n）-f（n-1），

所以f（n）-f（n-1）≥f（n-1）-f（n-2）≥… ≥f（i）-f（i-1）>0，

所以f（n）=[f（n）-f（n-1）]+…+[f（i+1）-f（i）]+f（i）>0，

与f（n）=0矛盾，

所以，对任意的i∈{1，2，3，…，n-1}有f（i）≤0。

（3）不成立

例如

证明：当x为有理数时，x-1，x+1均为有理数，

f（x-1）+f（x+1）-2f（x）=（x-1）²+（x+1）²-2x²-n（x-1+ x+1-2x）=2

当x为无理数时，x-1，x+1均为无理数，

f（x-1）+f（x+1）-2f（x）=（x-1）²+（x+1）²-2x²=2，

所以，函数f（x）对任意的x∈R，均有f（x-1）+f（x+1）≥2f（x），

即函数f（x）具有性质P

而当x∈[0，n]（n>2）且当x为无理数时，f（x）>0

所以，在（2）的条件下，“对任意x∈[0，n]均有f（x）≤0”不成立。