问题
单项选择题
已知α1(-3，2，0)T，α2(-1，0，-2)T是线性方程组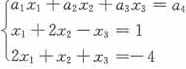
的两个解，那么方程组的通解是（）。
A．(-3，2，0)T+k(-1，1，1)T
B．(2，1，0)T+k(1，-1，0)T
C．(2，-1，0)T+k(-1，0，1)T
D．(-2，0，3)T+k(0，1，-1)T
答案
参考答案：A
解析：
因为α1，α2是AX=b的两个不同的解，故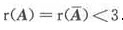
。又因为行列式|A|中有2阶子式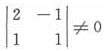
知r(A)≥2，从而r(A)=2
那么，导出组AX=0的基础解系只有n-r(A)=1个解向量，
α1-α2=(-2，2，2)T是AX=0的解，按解的结构知
(-3，2，0)T+k(-1，1，1)T
是方程组的通解，故正确答案为A。