问题
问答题
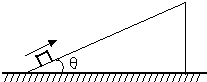
一个物体从倾角为θ=37°的斜面底端以v0=10m/s的初速度沿斜面向上滑动,设物体与斜面间的动摩擦因数为μ=0.5,已知斜面足够长.求
(1)物体上滑的加速度大小;
(2)物体沿斜面上滑的最大位移的大小;
(3)物体能再滑回底端吗?若能,经多长时间滑回底端?
(sin37°=0.6,cos37°=0.8,g=10m/s2)
答案
(1)物体上滑时,受到重力、斜面的支持力和沿斜面向下的滑动摩擦力,根据牛顿第二定律得,物体上滑过程的加速度大小为
a=
=g(sinθ+μcosθ)mgsinθ+μmgcosθ m
代入解得,a=10m/s2.
(2)由运动学公式得:0-
=-2ax得v 20
x=v 20 2a
代入解得,x=5m
(3)最大静摩擦力近似等于滑动摩擦力,物体到达最高点时最大静摩擦力fm=μmgcosθ=0.4mg,重力沿斜面向下的分力为mgsinθ=0.6mg
所以mgsinθ>fm,物体将滑回斜面底端.
下滑过程中,加速度大小为a′=
=g(sinθ-μcosθ)=2m/s2.mgsinθ-μmgcosθ m
由x=
a′t2得,t=1 2
=2x a′
s=2×5 2
s5
答:
(1)物体上滑的加速度大小为10m/s2;
(2)物体沿斜面上滑的最大位移的大小5m;
(3)物体能再滑回底端.经
s的时间滑回底端.5
