问题
选择题
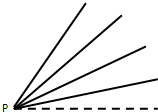
如图所示,几条足够长的光滑直轨道与水平面成不同角度,从P点以大小不同的初速度沿各轨道发射小球,若各小球恰好在相同的时间内达到各自的最高点,则各小球最高点的位置( )
A.在同一水平线上
B.在同一竖直线上
C.在同一圆周上
D.在同一抛物线上
答案
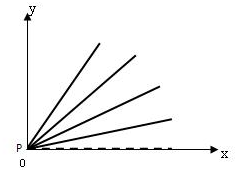
建立如图所示的直角坐标系,设小球在任一斜面上最高点的坐标为(x,y),根据牛顿第二定律得到
小球在此斜面上加速度的大小为
a=g
,x x2+y2
由运动学公式得:小球在斜面上运动的位移为:
=x2+y2
at2联立得到:1 2
=x2+y2
•1 2
•t2x x2+y2
得到,2x2+2y2-gt2x=0,
式中a、t是定值,根据数学知识得知,此方程是圆.所以各小球最高点的位置在同一圆周上.
故选C
