问题
填空题
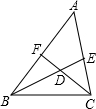
已知BE、CF是△ABC的角平分线，BE、CF相交于点D，若∠A=50°，则BE与CF相交所成的角为 。
答案
115°、65°
分析：根据三角形内角和定理可求得∠ABC+∠ACB的度数，再根据角平分线的定义可求得∠OBC+∠OCB的度数，最后根据三角形内角和定理即可求解．
解答：解：∵在△ABC中，∠A=50°，∠ABC+∠ACB+∠A=180°，
∴∠ABC+∠ACB=130°；
又∵角平分线BE、CF相交于D，
∴∠DBC+∠DCB=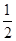
（∠ABC+∠ACB）=65°，
∴∠BDC=180°-65°=115°，
∠EDC=180°-∠BDC=65°；
故答案是：115°或65°．