问题
问答题
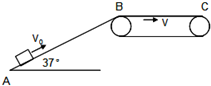
如图所示,一物体以初速度V0=10m/s冲上长度为SAB=5m的粗糙斜面,斜面与水平面的夹角=37°,斜面的末端B与传送带用光滑弧形相接,传送带始终保持v=2m/s的速率顺时针运行.已知传送带长度SBC=3m,物体与斜面及传送带间的动摩擦因数均为=0.5.试求:
(1)物体在斜面滑动时加速度a1的大小;
(2)物体刚滑上传送带时加速度a2的大小;
(3)物体从A运动到C所用的时间t.
答案
(1)根据牛顿第二定律得,a1=
=gsin37°+μgcos37°=10m/s2.mgsin37°+μmgcos37° m
(2)物块滑动到B点的速度为v,
有v2-v02=-2asAB
解得v=0
滑上传送带先做匀加速直线运动,加速度a2=
=μg=5m/s2.μmg m
(3)物体从A运动到B的时间t1=
=0-v0 -a
s=1s.-10 -10
物块在传送带上匀加速直线运动的时间t2=
=v a2
s=0.4s.2 5
在这段时间内物体的位移x1=
=v2 2a2
m=0.4m4 10
则物体在传送带上匀速直线运动的时间t3=
=sBC-x1 v
s=1.3s3-0.4 2
所以总时间t=t1+t2+t3=2.7s.
答:(1)物体在斜面滑动时加速度a1的大小10m/s2
(2)物体刚滑上传送带时加速度a2的大小5m/s2
(3)物体从A运动到C所用的时间t=2.7s.
