问题
填空题
等腰三角形的腰长为10，底边长为12，则等腰三角形的面积为 ▲ 。
答案
48
A作AD⊥BC于D，根据等腰三角形性质求出BD，根据勾股定理求出AD，根据三角形的面积公式求出即可．
解： 过A作AD⊥BC于D，
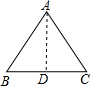
∵AB=AC，AD⊥BC，
∴BD=DC=6，
由勾股定理得：AD=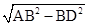
=8，
∴△ABC的面积是S=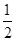
BC×AD=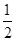×12×8=48，
搜题请搜索小程序“爱下问搜题”
等腰三角形的腰长为10，底边长为12，则等腰三角形的面积为 ▲ 。
48
A作AD⊥BC于D，根据等腰三角形性质求出BD，根据勾股定理求出AD，根据三角形的面积公式求出即可．
解： 过A作AD⊥BC于D，
∵AB=AC，AD⊥BC，
∴BD=DC=6，
由勾股定理得：AD=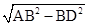=8，
∴△ABC的面积是S=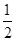BC×AD=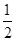×12×8=48，