问题
填空题
AD、BE、CF为△ABC的内角平分线.若BD+BF=CD+CE=AE+AF,则∠BAC的度数为 .
答案
60°
解:记BC=a,CA=b,AB=c.由内角平分线定理知
BD= 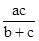 ,CD=
,CD=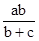 ,BF=
,BF=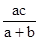 ,CE=
,CE=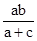 .
.
由BD+BF=CD+CE,.
去分母并化简得a2c+2ac2+2bc2+c3=a2b+2ab2+2b2c+b3,
即 (c-b)(a2+2ac+2ab+b2+c2+3bc)=0.
显然a2+2ac+2ab+2bc+b2+c2+bc=(a+b+c)2+bc>0.
于是,c-b=0,即b=c.
同理,当CD+CE=AE+AF时,有c=a.所以,a=b=c,△ABC为等边三角形.
故∠BAC=60°.
