(20分)已知△ABC中,∠A>∠B>∠C,且∠A=2∠B.若三角形的三边长为整数,面积也为整数,求△ABC面积的最小值.
记BC=a,CA=b,AB=c.
如图,作∠BAC的平分线AD,则∠BAD=∠DAC=∠B,
∠ADC=∠B+∠BAD=2∠B.
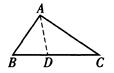
故△ACD△BCA.于是,b/a=CD/b.①
又由角平分线定理知b/c=CD/BD.从而, =
= =
=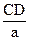 .②
.②
由式①、②得 =
= .
.
故a2=b(b+c).
若(b,c)=d,则由式①知d|a,故不妨设(b,c)=1.于是,可令
b=m2,b+c=n2.则a=mn,c=n2-m2.
由∠A>∠B>∠C,知a>b>c,即mn>m2>n2-m2.
故m<n< 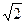 m.③
m.③
又m、n为正整数,从而, 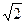 m-m>1,即m>
m-m>1,即m> 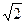 +1.④
+1.④
设△ABC的面积为S,由海伦公式知
S= n(n+m)(n-m)·
n(n+m)(n-m)·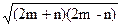 .
.
由式④知m≥3.又由式③容易验证:
当3≤m≤7时,只有m=5时,n=6,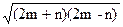 =8(有理数),此时,
=8(有理数),此时,
S=14×6×11×1×8=132.
下证当m≥8,n≥9时,S>162.
由式③、④知(2m+n)(2m-n)>3m(2m- 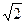 m)=(6-3
m)=(6-3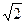 )m2>(6-4
)m2>(6-4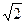 )m2=(2-
)m2=(2-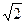 )2m2,
)2m2,
n(n+m)(n-m)>n(1+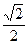 n)×1=
n)×1=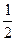 (2+
(2+ 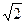 )n2.
)n2.
由式⑤知 S>14×12(2+ 2)n2(2- 2)m=14n2
则当m≥8,n≥9时,有S>162.
故S的最小值为132,此时,m=5,n=6.所以,a=30,b=25,c=11时,△ABC
面积最小,最小值为132.
