问题
解答题
已知函数f(x)=2x,
(1)求函数F(x)=f(x)+af(2x),x∈(-∞,0]的最大值;
(2)若存在x∈(-∞,0),使f(2x)-af(x)>1成立,求a的取值范围;
(3)若当x∈[0,3]时,不等式f(x+1)≤f[(2x+a)2]恒成立,求a的取值范围。
答案
解:(1)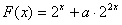 ,
,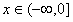
令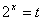
因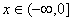
故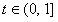
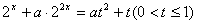
当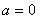 时,
时,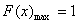
当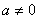 时,令
时,令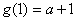
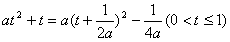
若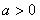 ,
,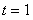 时,
时,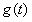 取得最大值,
取得最大值,
若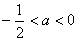 ,
,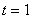 时
时 取得最大值,
取得最大值,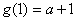
若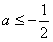 ,
,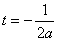 时
时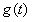 取得最大值,
取得最大值,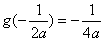
综上,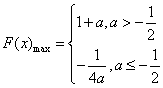 ;
;
(2)令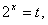 则存在
则存在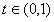 使得
使得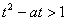
即存在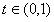 使得
使得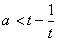
所以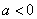
a的取值范围是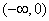 ;
;
(3)因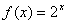 是单调增函数,故由
是单调增函数,故由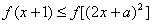 得
得
问题转化为 对
对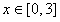 恒成立
恒成立
即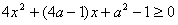
令
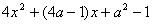
若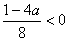 ,必需且只需
,必需且只需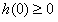 ,此时得
,此时得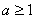 ;
;
若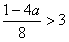 ,必需且只需
,必需且只需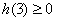 ,此时得
,此时得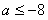 ;
;
若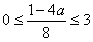 ,必需且只需
,必需且只需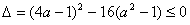 ,此时无解
,此时无解
综上得a的取值范围是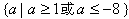 。
。
