问题
解答题
已知函f（x）=1﹣2ax﹣a2x（a＞1）
（1）求函f（x）的值域；
（2）若x∈[﹣2，1]时，函f（x）的最小值﹣7，求a的值和函f（x） 的最大值．
答案
解：设ax=t＞0
∴y=﹣t2﹣2t+1=﹣（t+1）2+2
（1）∵t=﹣1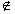
（1，+∞）
∴y=﹣t2﹣2t+1在（0，+∞）上是减函数
∴y＜1所以值域为（﹣∞，1）
（2）∵x∈[﹣2，1]，a＞1
∴t∈[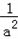
，a]
由t=﹣1
[
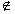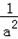，a]
∴y=﹣t2﹣2t+1在[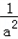
，a]上是减函数
∵﹣a2﹣2a+1=﹣7
∴a=2或a=﹣4（不合题意舍去）
当t=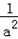
=
时，y有最大值，ymax=﹣（
）2﹣2×
+1=