问题
填空题
AD是△ABC边BC的中线,若AB=4, AC=2;则中线AD的取值范围是
答案
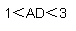
求中线AD的取值范围可延长AD至点E,使AD=DE,得出△ACD≌△EBD,进而在△ABE中利用三角形三边关系求解..
解:画出图形如右所示,
延长AD至点E,使AD=DE,连接BE,
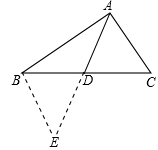
∵AD是△ABC的边BC上的中线,
∴BD=CD,
又∠ADC=∠BDE,AD=DE
∴△ACD≌△EBD,
∴BE=AC,
在△ABE中,AB-BE<AE<AB+BE,
即AB-AC<AE<AB+AC,4-2<AE<4+2,
∴2<AE<6,
∴1<AD<3..