答案：C

确定A、B两点的位置，分别以AB为腰、底讨论C点位置．

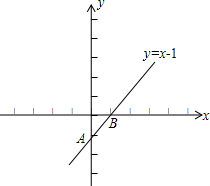
解：直线y=x-1与y轴的交点为（0，-1），直线y=x-1与x轴的交点为（1，0）．

①以AB为底，C在原点；

②以AB为腰，且A为顶点，C点有3种可能位置；

③以AB为腰，且B为顶点，C点有3种可能位置．

所以满足条件的点C最多有7个：（0，0），（0，1），（-1，0），[0，（-1-）]，

[（1+），0]，[（1-），0]，[0，（-1）]

故选C．

本题考查了一次函数图象上点的坐标特征、等腰三角形的判定．底和腰不等的等腰三角形，若条件中没有明确哪边是底哪边是腰时，应在符合三角形三边关系的前提下分类讨论．