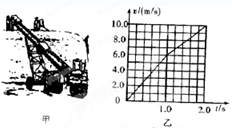
（1）皮带的速度为6.0 m/s，方向沿斜面向下．

（2）由货物运动的v-t图象得：a₁=

△v1

△t1

=6.0 m/s²，a₂=

△v2

△t2

=4.0 m/s²．

在0～1.0 s：皮带对物体的滑动摩擦力沿斜面向下，由牛顿第二定律得：mg•simθ+μmg•cosθ=ma₁．

在1.0 s～2.0 s：皮带对物体的滑动摩擦力沿斜面向上，由牛顿第二定律得：mg•sinθ-μmg•cosθ=ma₂．

联立得：θ=30°，μ=

3

15

=0.115．

（3）由v-t图象知货物在1.0时间内加速到与皮带相同的速度6.0 m/s，皮带发生的位移s_带=v₁t=6.0 m，货物发生的位移s_物=

v1

2

•t=3.0 m，此时间内皮带上痕迹的长度：△s=s_带-s_物=3.0 m＜l=4.0 m．

此后货物速度超过皮带速度，物体向底端运动过程中发生的距离比皮带多4.0 m（其中有3.0 m为痕迹重叠区域）．设从1.0秒末开始，货物的传送到底端的时间为t₁、货物到底端的距离为S，则：

对皮带S-4=v₁t₁，对货物S=v₁t₁+

1

2

a₂

t

21

，联立以上两式得：t₁=

2

s=1.41 s，l=（6

2

+4）m=12.46 m，

故每件货物的传送时间：T=t₁+t=（1+

2

）s=2.41 s，传送距离：L=s_物+S=15.46 m．

答：（l）皮带的速度为6.0m/s；

（2）皮带与水半面间的夹角θ为30度，货物与皮带之间的动摩擦因数μ的大小为0.115；

（3）该件货物的传送时间为2.41s，传送距离为15.46m．