问题
填空题
在△ABC中,E是AB上一点,AE=2,BE=3,AC=4,在AC上取一点D,使以A、D、E为顶点的三角形与△ABC相似,则AD的 值是 .
答案
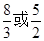
因为AB和AC、AD和AE有共同的夹角∠A,故使得  =
= 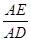 或
或 =
= 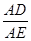 ,即可求出AD的长度,即可解题.
,即可求出AD的长度,即可解题.
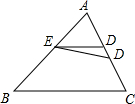
解:∵AB和AC、AD和AE有共同的夹角∠A,
∴ =
= 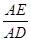 或
或 =
= 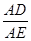 ,均可使得△ADE和△ABC相似,
,均可使得△ADE和△ABC相似,
解得AD=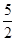 或
或 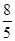 .
.
故答案为: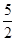 或
或 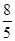 .
.
此题考查了相似三角形对应边比值相等的性质,本题中讨论 =
= 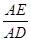 或
或 =
= 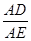 是解题的关键.
是解题的关键.
