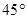或．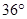

MN是AB的中垂线，则△ABN是等腰三角形，且NA=NB，即可得到∠B=∠BAN=∠C．然后对△ANC中的边进行讨论，然后在△ABC中，利用三角形内角和定理即可求得∠B的度数．

解：∵把△ABC折叠，使点B与点A重合，折痕交AB于点M，交BC于点N，

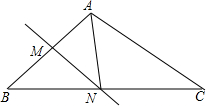
∴MN是AB的中垂线．

∴NB=NA．

∴∠B=∠BAN，

∵AB=AC

∴∠B=∠C．

设∠B=x°，则∠C=∠BAN=x°．

1）当AN=NC时，∠CAN=∠C=x°．

则在△ABC中，根据三角形内角和定理可得：4x=180，

解得：x=45°则∠B=45°；

2）当AN=AC时，∠ANC=∠C=x°，而∠ANC=∠B+∠BAN，故此时不成立；

3）当CA=CN时，∠NAC=∠ANC=．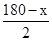

在△ABC中，根据三角形内角和定理得到：x+x+x+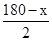=180，

解得：x=36°．

故∠B的度数为 45°或36°．