问题
解答题
已知盘中有编号为A,B,C,D的4个红球,4个黄球,4个白球(共 12个球)现从中摸出4个球(除编号与颜色外球没有区别) （12分）
（1）求掐好包含字母A, B,C,D的概率;
（2）设摸出的4个球中出现的颜色种数为随机变量X.求X的分布列和期望E(X).
答案
（1）
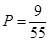；（2）分布列见解析，期望
.
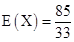题目分析：（1）按分步乘法原理，可求出恰好包含字母A, B,C,D的事件个数为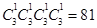
，从12个球中摸出4个球的个数为
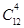，相除可得概率；（2）摸出的4个球中出现的颜色种数为随机变量X，可能取值为
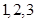分别求出概率，列出分布列，进一步求出期望.
试题解析：(Ⅰ) P=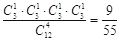
--------------4分
（2）
,
,
.
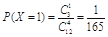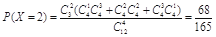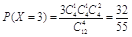分布列为:
| X | 1 | 2 | 3 |
| P |  |  |  |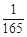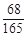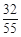
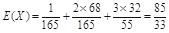12分