某公用事业公司拟建一个火力发电厂,投资规模视筹资情况而定,如果金融市场有大量游资,可能筹集资金300万,概率为0.5;若资金市场资金供需平衡,能筹资200万,概率为 0.4;若资金供应紧张,能筹资100万,概率为0.1。项目建成后的年收入与发电规模有直接关系,同时还受电力市场供求状况的影响,在市场状况良好时,年收入为投资规模的40%,概率为0.3;市场状况一般时,年收入为投资规模的30%,概率为0.5;市场萧条时,年收入为投资规模的20%,概率为0.2。该发电厂的年运营费用受煤炭供求关系影响,煤炭供应充足时,年运行费为投资规模的5%,概率为0.2;煤炭供求平衡时,年运行费为投资规模的10%,概率为 0.5;煤炭供应紧张时,年运行费为投资规模的15%,概率为0.3。该项目的基准贴现率为 10%,项目计算期为10年,期末无残值。
试计算该项目的期望净现值及净现值非负的累计概率。
参考答案:
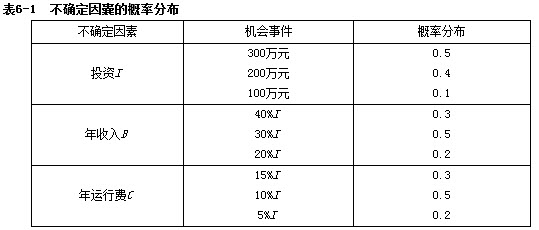
确定不确定因素及其概率分布(见表6-1)
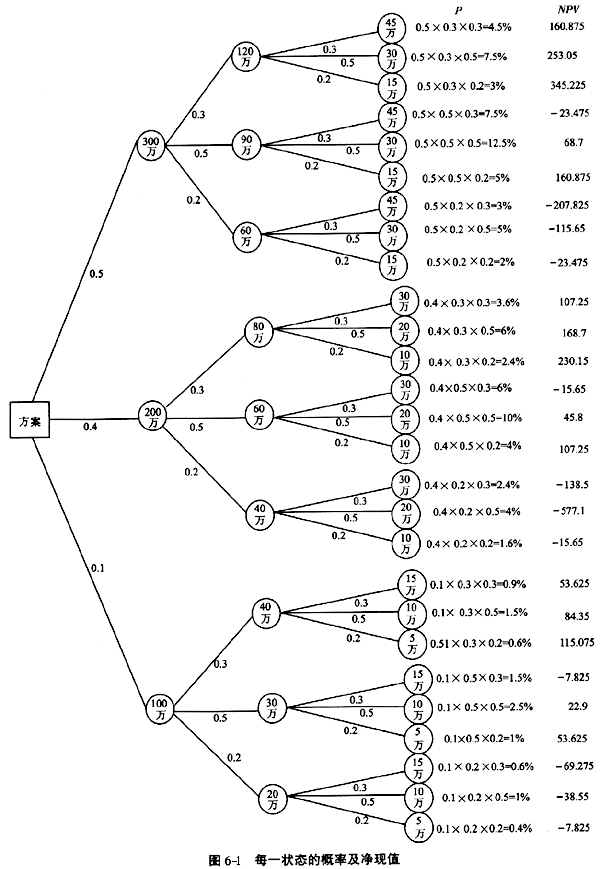
2.利用决策树技术确定每一状态的概率及净现值(见图6-1)
在图6-1中,各状态的概率等于个阶段概率之积,如投资为300万元,收入为120万元,费用为45万元的概率:
A3=P(I=300)×P(B=120)×p(C=45)
=0.5×0.3×0.3=4.5%
其他状态的概率计算亦如图6-1所示。
各状态的净现值计算:
NPVi=(B-C)(P/A,10%,10)-I
=(120-45)×6.145-300
=160.875
3.计算期望净现值
E(NPV)= 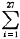 Pi|NPVi≥0=64.647
Pi|NPVi≥0=64.647
4.计算净现值非负的累计概率
P(NPV>0)=  (Pi|NPVi≥0)=65%
(Pi|NPVi≥0)=65%
或P(NPV>0)=1-P(NPV<0)=65%
项目可行的概率为65%,刚过半数多一点,说明项目风险较大。
