问题
填空题
一个等腰三角形的底角为15°，腰长为4cm，那么，该三角形的面积等于 .
答案
4
首先根据题意作图，然后过点C作CD⊥AB于D，即可得∠CAD=30°，由直角三角形中，30°角所对的直角边是其斜边的一半，即可求得△ABC的高CD的长，则可求得这个三角形的面积．
解：如图：AC=AB=4cm，∠B=∠ACB=15°，
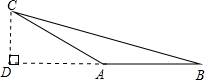
过点C作CD⊥AB于D，
∴∠CAD=∠ACB+∠B=15°+15°=30°，
∴CD=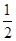
AC=2cm（在直角三角形中，30°角所对的直角边是斜边的一半），
∴S△ABC=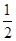AB?CD=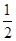×4×2=4（cm2）．
∴这个三角形的面积为4cm2．
故答案为：4cm2．