问题
问答题
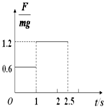
在消防演习中,消防队员从一根竖直的长直轻绳上由静止滑下,经一段时间落地.为了获得演习中的一些数据,以提高训练质量,研究人员在轻绳上端安装一个力传感器并与数据处理系统相连接,用来记录消防队员下滑过程中轻绳受到的拉力与消防队员重力的比值随时间变化的情况.已知某队员在一次演习中的收集的数据如图所示,g取10m/s2.
(1)求该消防队员在下滑过程中的最大速度和落地速度各是多少?
(2)消防队员在下滑过程的总位移?
答案
(1)设该消防队员先在t1=1s时间内以加速度大小a1匀加速下滑.然后在t2=1.5s时间内以加速度大小a2匀减速下滑.
前1s内,由牛顿第二定律得:
mg-F1=ma1
得,a1=g-
=4m/s2F1 m
所以消防队员的最大速度vm=a1t1
代入数据解得:vm=4m/s
后1.5s内,由牛顿第二定律得:
F2-mg=ma2
得,a2=
-g=2m/s2F2 m
队员落地时的速度v=vm-a2t2
代入数据解得:v=1m/s
(2)t1=1s时间内,下落位移为x1=
a1t12=1 2
×5×12m=2.5m1 2
后1.5s内,下落的位移为x2=
t2=vm+v 2
×1.5m=3.75m4+1 2
故总位移为x=x1+x2=6.25m
答:(1)该消防队员在下滑过程中的最大速度和落地速度各是4m/s和1m/s.
(2)消防队员在下滑过程的总位移是6.25m.
