问题
解答题
深圳市某校中学生篮球队假期集训,集训前共有6个篮球,其中3个是新球(即没有用过的球),3个是旧球(即至少用过一次的球).每次训练,都从中任意取出2个球,用完后放回.
(1)设第一次训练时取到的新球个数为ξ,求ξ的分布列和数学期望;
(2)求第二次训练时恰好取到一个新球的概率.
答案
(1)ξ的分布列为
| ξ | 0 | 1 | 2 |
| P | 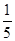 | 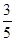 | 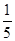 |
ξ的数学期望为E(ξ)=1
(2)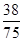
(1)ξ的所有可能取值为0,1,2.
设“第一次训练时取到i个新球(即ξ=i)”为事件Ai(i=0,1,2).
∵集训前共有6个篮球,其中3个是新球,3个是旧球,
∴P(A0)=P(ξ=0)=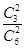 =
=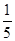 ,
,
P(A1)=P(ξ=1)=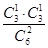 =
=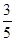 ,
,
P(A2)=P(ξ=2)=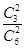 =
=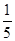 .
.
∴ξ的分布列为
| ξ | 0 | 1 | 2 |
| P | 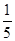 | 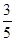 | 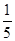 |
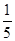 +1×
+1×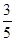 +2×
+2×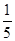 =1.
=1.(2)设“从6个球中任意取出2个球,恰好取到一个新球”为事件B.
则“第二次训练时恰好取到一个新球”就是事件A0B+A1B+A2B.而事件A0B,A1B,A2B互斥,
∴P(A0B+A1B+A2B)=P(A0B)+P(A1B)+P(A2B).
由条件概率公式,得
P(A0B)=P(A0)P(B|A0)=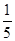 ×
×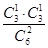 =
=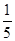 ×
×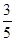 =
=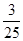 ,
,
P(A1B)=P(A1)P(B|A1)=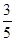 ×
×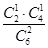 =
=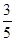 ×
×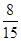 =
=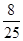 ,
,
P(A2B)=P(A2)P(B|A2)=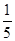 ×
×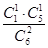 =
=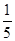 ×
×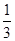 =
=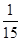 ,
,
∴第二次训练时恰好取到一个新球的概率为
P(A0B+A1B+A2B)=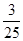 +
+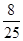 +
+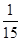 =
=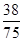 .
.
