问题
问答题
(Ⅰ)证明积分中值定理：若函数f(x)在闭区间[a，b]上连续，则至少存在一点η∈[a，b]，使得
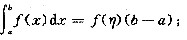
(Ⅱ)若函数ψ(x)具有二阶导数，且满足
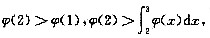则至少存在一点ξ∈(1，3)，使得ψ"(ξ)＜0．
答案
参考答案：[证明] (Ⅰ)由函数f(x)在闭区间[a，b]上连续知，存在f(x)在[a，b]上的最大值M与最小值m，即对[*]有m≤f(x)≤M．从而由定积分的性质可得
[*]
这表明[*]是f(x)值域[m，M]上的一个值．由闭区间上连续函数的性质知：[*]使得
[*]
(Ⅱ)由(Ⅰ)的结论知，[*]
[*]
分别在区间[1，2]与[2，η上对ψ(x)应用拉格朗日中值定理即得：[*]ξ1∈(1，2)与ξ2∈(2，η)分别使得
[*]
再在区间[ξ1，ξ2]上对导函数ψ’(x)应用拉格朗日中值定理，就有ξ∈(ξ1，ξ2)[*](1，3)使得
[*]