问题
问答题
设函数u=f(x，y)具有二阶连续偏导数，且满足等式
确定a，b的值，使等式在变换ξ=z+ay，η=x+by下简化为
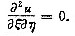
答案
参考答案：求解本题的关键是用u对ξ，η的一、二阶偏导数来表示三个二阶偏导数[*]利用多元复合函数求偏导数的链式法则可得
[*]
[*]
注意在上面的计算中应用了连续的二阶混合偏导数[*]
把以上结果代入原等式可得
[*]
选取a与b同时满足5a2+12a+4=0与5b2+126+4=0可得a与b均可取-2或[*]由于当a=b=-2或[*]时，10ab+12(a+b)+8=0，而当a=-2，[*]时10ab+12(a+b)+8≠0，可知当a=-2与[*]