参考答案：B

解析：

[分析]： 根据前序、后序遍历的特点，可以确定A是根结点(在后序遍历的最后一个)，再根据中序遍历的特点，可以知道DBGEHJ为左子树，CIF为右子树。

再看右子树的后序遍历为IFC，可以确定C为右子树的根结点；再加上中序为CIF，说明C无左子树，只有右子树。

而左子树的后序遍历为DGJHEB，因此B为左子树的根结点，再结合中序遍历，可以得知B的左子树只有D，GEHJ都是右子树。

GEHJ子树的后序遍历是GJHE，说明E是根，HJ为E的右子树，G是E的左子树。最后可知H为HJ子树的根，J为右子树。

通过以上分析，可以绘制出这棵树，如图所示。

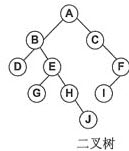
再由前序遍历，可以得到ABDEGHJCFI。