设φ(X)=XAXT，ψ(X)=XAXT是正定二次型，其中A=(aij)，B=(bi

问题问答题

设φ(X)=XAX^T，ψ(X)=XAX^T是正定二次型，其中A=(a_ij)，B=(b_ij)，令c_ij=a_ijb_ij，以C=(c_ij)作二次型f(X)=XCX^T．
证明：f是正定的．

答案

参考答案：对于正定矩阵B=(b_ij)，存在满秩矩阵P=(p_ij)，使得

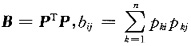，于是

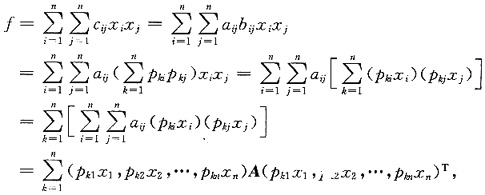
因为A正定，所以对任一(p_k1x₁，p_k2x₂，…，p_knx_n)^T≠0，有
(p_k1x₁，p_k2x₂，…，p_knx_n)A(p_k1x₁，p_k2x₂，…，p_knx_n)^T＞0，
又因为P满秩，于是，对任一非零向量X=(x₁，x₂，…，x_n)，有PX^T≠0，
则(p_k1x₁，p_k2x₂，…，p_knx_n)(k=1，2，…，n)不全为零，故f正定．