问题
问答题
证明:当x>0时,不等式
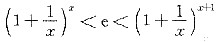 成立.
成立.
答案
参考答案:设[*]则
[*]
因此f’1(x)是单调递减的.而
[*]
可见,对任何x>0,均有f’1(x)>0.所以f1(x)在x>0时是单调递增的,也就有[*]为单调递增的.又已知[*]所以就有对x>0,[*]
现在来证明不等式的另一半.
设[*]则
[*]
因此f’2(x)是单调递增的,而
[*]
可见,对任何x>0,均有f’2(x)<0。所以f2(x)在x>0时是单调递减的,即有[*]为单调递减的.已知[*]所以对x>0,[*]
解析:
[分析]: 当x>0时,[*]均具有单调性,也就是它们的导数均为正或负,为了求导方便,它们的单调性可以从它们取对数后的单调性判定,因为对数函数本身就具有单调性.
