问题
问答题
设λ1=3,λ2=6,λ3=9是三阶实对称矩阵A的三个特征值,其对应的特征向量依次为

证明:(Ⅰ)
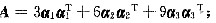
(Ⅱ)把β=(1,2,3)T用α1,α2,α3线性表出,并求Anβ.
答案
参考答案:[*]
[*]
(Ⅱ)令β=x1α1+x2α2+x3α3[*]x1=1,x2=3,x3=2.
于是有 β=α1+3α2+2α3,从而
[*]
解析:
[分析]: 已知特征值、特征向量反求矩阵也是一种常见题型.
