问题
问答题
设a0=4,a1=1,an-2=n(n-1)an,n≥2.
求幂级数[*]的和函数S(x);
答案
参考答案:设幂级数
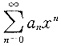 的收敛区间为(-R,R),逐项求导得
的收敛区间为(-R,R),逐项求导得
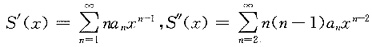 ,
,
又 an-2=n(n-1)an,n≥2,
所以
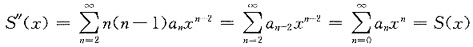 ,
,
即 S"(x)-S(x)=0,解之得S(x)=C1ex+C2e-x,
代入S(0)=a0=4,S’(1)=a1=1可解得
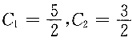 ,
,
所以
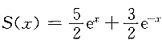 .
.
设a0=4,a1=1,an-2=n(n-1)an,n≥2.
求幂级数[*]的和函数S(x);
参考答案:设幂级数
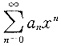 的收敛区间为(-R,R),逐项求导得
的收敛区间为(-R,R),逐项求导得
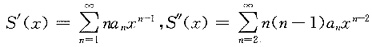 ,
,
又 an-2=n(n-1)an,n≥2,
所以
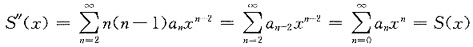 ,
,
即 S"(x)-S(x)=0,解之得S(x)=C1ex+C2e-x,
代入S(0)=a0=4,S’(1)=a1=1可解得
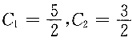 ,
,
所以
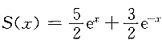 .
.