问题
单项选择题
已知函数y=f(x)对一切x满足xf"(x)+3x[f’(x)]2=1-e-x,若f’(x0)=0(x0≠0),则
A.f(x0)是f(x)的极大值.
B.(x0,f(x0))是曲线y=f(x)的拐点.
C.f(x0)是f(x)的极小值.
D.f(x0)不是f(x)的极值,(x0,f(x0))不是曲线y=f(x)的拐点.
答案
参考答案:C
解析:[详解] 由题设可得
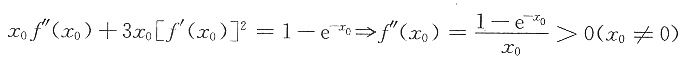 ,
,
所以f(x0)是f(x)极小值,即选(C).
