问题
问答题
已知点A(1，0，0)与点B(1，1，1)，Σ是由直线AB绕Oz轴旋转一周而成的旋转曲面介于平面z=0与z=1之间部分的外侧，函数f(u)在(-∞，+∞)内具有连续导数，计算曲面积分
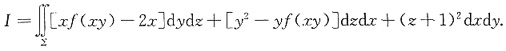
答案
参考答案：直线AB的方程为
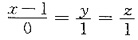
则直线
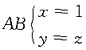绕Oz轴旋转一周而成的旋转曲面方程为
x2+y2=1+z2，即x2+y2-z2=1
记P=xf(xy)-2x，Q=y2-yf(xy)，R=(z+1)2，则
，
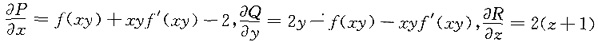于是
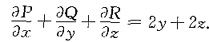
补面Σ1：z=0(x2+y2≤1)，下侧，Σ2：z=1(x2+y2≤2)，上侧．由高斯公式得
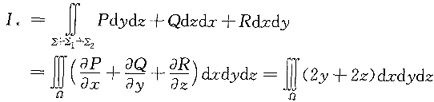
由对称性知
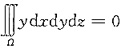，利用截面法可得
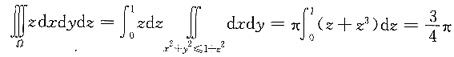
故
．
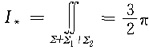又
，
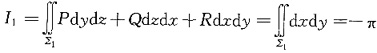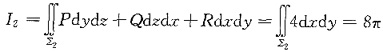
所以，
．
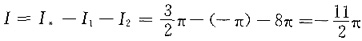