问题
单项选择题
已知实二次型
f=(a11x1+a12x2+a13x3)2+(a21x1+a22x2+a23x3)2+(a31x1+a32x2+a33x3)2正定,矩阵A=(aij)3×3,则
A.A是正定矩阵.
B.A是可逆矩阵.
C.A是不可逆矩阵.
D.以上结论都不对.
答案
参考答案:B
解析:[详解] 令x=(x1,x2,x3)T,
则f=xTATAx=(Ax)TAx正定
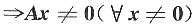 ,
,
即Ax=0只有零解,即A可逆,故选(B).
