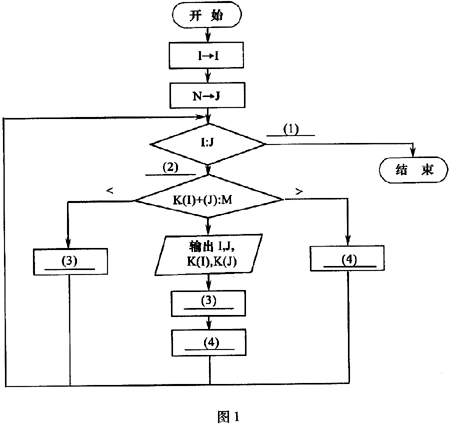
参考答案：(1)≥ (2)＜ (3)I+1-＞I (4)J-1-＞J (5)[N/2]

解析： 该算法的思路是：设置了两个变量I和J，初始时分别指向数组K的第一个元素和最后一个元素。如果这两个元素之和等于M时，输出结果，并这两个指针都向中间移动；如果小于M，则将指针I向中间移动(因为数组K已按从小到大的顺序排列)；如果大于M，则将指针J向中间移动(因为数组K已按从小到大的顺序排列)。当I≥J时，说明所有的元素都搜索完毕，退出循环。
根据上面的分析，(1)、(2)空要求填写循环结束条件，显然，(1)空处应填写“≥”，(2)空处应填写“＜”。这里主要要注意I=J的情况，当I=J时，说明指两个指针指向同一元素，应当退出循环。
(3)空在流程图有两处，一处是当K(I)+K(J)=M时，另一处是当K(I)+K(J)＜M时，根据上面分析这两种情况都要将指针I向中间移动，即“I+1-＞I”。同样的道理，(4)空处应填写“J-1-＞J”。
比较“K(I)+K(J)：M”最少执行次数发生在第1元素与第N个元素之和等于M、第2元素与第N-1个元素之和等于M、……，这样每次比较，两种指针都向中间移动，因此最小执行次数约为“N-2”。