问题
问答题
已知二维向量α不是二阶方阵A的特征向量，
(Ⅰ)证明α，Aα线性无关；
(Ⅱ)若A2α+Aα-6α=0，求A的全部特征值，并判断A能否与对角矩阵相似。
答案
参考答案：设k1α+k2Aα=0，则k2=0，否则
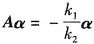，α是的A特征向量，与题设矛盾，将k2=0代入k1α+k2Aα=0，得k1α=0，又α≠0，故k1=0，所以α，Aα线性无关；
(Ⅱ)A2α+Aα-6α=0
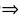(A2+A-6E)α=0
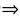(A+3E)(A-2E)α=0或(A-2E)(A+3E)α=0，(A+3E)(A-2E)α=(A+3E)(Aα-2α)=0，又Aα-2α≠0，故(A+3E)有一个特征值为0，从而A有一个特征值为-3，
同理，A-2E有一个特征值为0，从而A有一个特征值为2，故A的特征值为-3和2。
由于二阶方阵A有两个不同的特征值，故A能与对角矩阵相似。
解析：[考点]