问题
问答题
设f(x)为连续的周期函数,周期为T,求证
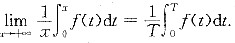
答案
参考答案:证法一 对于任意充分大的x>0,存在正整数n,使
nT≤x<(n+1)T.
显然,当x→+∞时,有n→+∞,当n→+∞时,有x→+∞.
设x=nT+S(0≤S<T),若左端极限存在,则必有
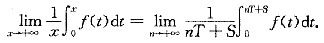
记
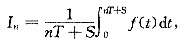
则
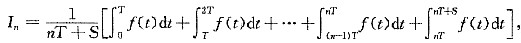
即
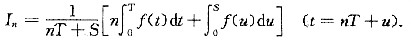
根据积分中值定理有

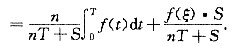
故
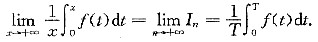
(因f(x)连续,x∈[0,T,故f(x)有界,x∈E0,T])
证法二 设

则

即
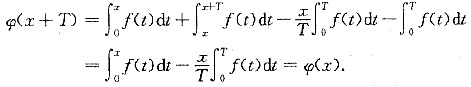
即φ(x)也是周期为T的连续函数,由连续性可知,φ(x)在[0,T]上有界,即存在M>0,|φ(x)|≤M,由周期性知.V
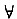 x,皆有|φ(x)|≤M.于是有
x,皆有|φ(x)|≤M.于是有
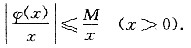
当x→+∞,有
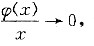
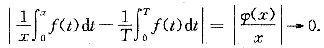
从而当x→+∞,有
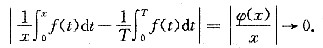
因此
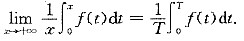
解析:
[分析]: f(x)连续,f(x+T)=f(x),T>0.
注:在证φ(x+T)=φ(x)的过程中,用到
[*]
注意到[*]
利用定积分的性质可以证明本命题,或采用辅助函数以及f(x)的周期性来证明.
注:在证φ(x+T)=φ(x)的过程中,用到
[*]
