问题
问答题
设x0>0,
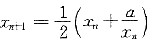 (n=0,1,2,…),且a>0,试证
(n=0,1,2,…),且a>0,试证
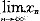 存在,并求此极限.
存在,并求此极限.
答案
参考答案:由题设x0>0,算术平均值不小于几何平均值,有
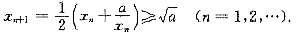
又
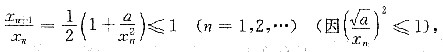
故数列{xn}单调递减且有下界,于是根据极限存在准则知
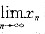 存在.
存在.
记
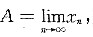 则
则
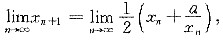
即
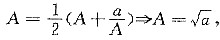
故

解析:
[分析]: 根据极限存在准则,证明数列有极限,再由递推关系式求出极限值.
设x0>0,
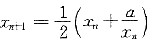 (n=0,1,2,…),且a>0,试证
(n=0,1,2,…),且a>0,试证
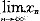 存在,并求此极限.
存在,并求此极限.
参考答案:由题设x0>0,算术平均值不小于几何平均值,有
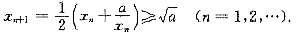
又
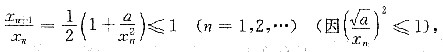
故数列{xn}单调递减且有下界,于是根据极限存在准则知
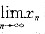 存在.
存在.
记
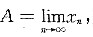 则
则
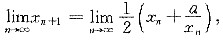
即
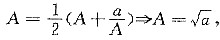
故

解析:
[分析]: 根据极限存在准则,证明数列有极限,再由递推关系式求出极限值.