问题
问答题
设D1是由抛物线y=2x2和直线x=a，x=2及y=0所围成的平面区域，D2是由y=2x2和直线y=0，x=a以所围成的平面区域，其中0＜a＜2．
(Ⅰ)试求D1绕x轴旋转而成的旋转体的体积V1，D2绕y轴旋转而成的旋转体的体积V2；
(Ⅱ)问当a为何值时，V1+V2取得最大值求此最大值．
答案
参考答案：
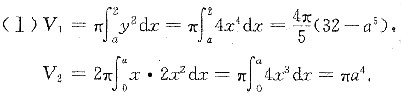
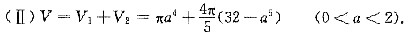
令 V’=4πa3(1-a)=0
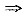a=0(舍去)，a=1∈(0，2)，故a=1为唯一驻点．
而 V"(1)=-4π＜0，
故a=1是V的极大值点，也即最大值点，此时最大值为
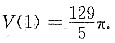
解析：
[分析]： 由题意知V1，V2都与a有关。故V1+V2是a的函数．于是本题应先求出V1+V2的表达式，然后再按照求函数最大值的方法，求出V1+V2的最大值点和最大值．