问题
填空题
已知二次型f(x1,x2,x3)=xTAx=2x12+2x22+ax23+4x1x3+2tx2x3经正交变换x=Py可化成标准形f=y12+2y22+7y32,则t=______.
答案
参考答案:±1
解析: 因为二次型xTAx经正交变换化为标准形时,标准形中平方项的系数就是二次型矩阵A的特征值,所以1,2,7是A的特征值.又因经过正交变换二次型的矩阵不仅合同而且还相似,因此有
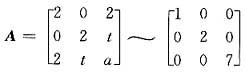
根据相似矩阵的性质,有
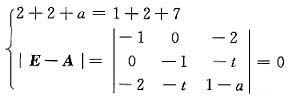
即:a=6,t2=1,所以应填±1.
注意求正交变换下二次型xTAx的标准形就是求二次型矩阵A的特征值,而告诉你正交变换下的标准形也就是告诉你特征值.如果本题求行列式|A-3E|的值,你能立即说出答案是8吗
