问题
填空题
已知A是三阶实对称矩阵,特征值是1,3,-2,其中α1=(1,2,-2)T,α2=(4,-1,a)T分别是属于特征值λ=1与λ=3的特征向量,那么矩阵A属于特征值λ=-2的特征向量是______.
答案
参考答案:k(0,1,1)T,k≠0
解析: 因为A是实对称矩阵,不同特征值的特征向量相互正交,设λ=-2的特征向量是α3=(x1,x2,x3)T,那么
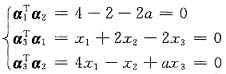
可先求出a=1,再由
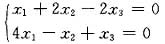
得到基础解系(0,1,1)T,所以α3(0,k,k)T,k≠0.
要掌握实对称矩阵特征值、特征向量的性质,除去正交性还有什么特性本题你能否求出矩阵A
