问题
填空题
已知
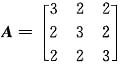，A*是A的伴随矩阵，那么A*的特征值是______．
答案
参考答案：1，7，7
解析： (解法一)按伴随矩阵定义，由代数余子式
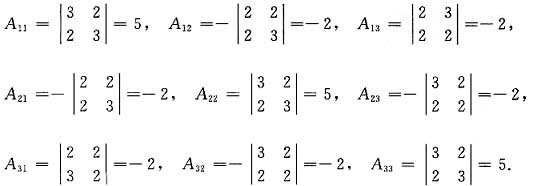
知伴随矩阵
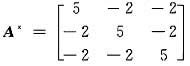
那么
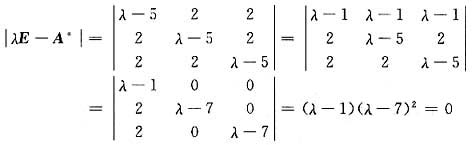
所以A*的特征值是1，7，7．
(解法二)由矩阵A的特征多项式
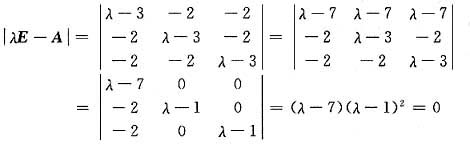
知矩阵A的特征值是7，1，1．
由|A|=
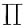λi，从而|A|=7·1·1=7．
因为若Aα=λα，则有A*α=
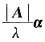．所以A*的特征值是1，7，7．
(解法三)因为
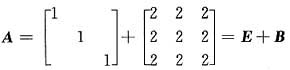
由秩r(B)=1，知B的特征值是6，0，0．故A的特征值是7，1，1．
解法一 用定义先求出伴随矩阵A*，再用特征多项式|λE-A*|求特征值，思路直接，但计算量大，繁琐．
解法二 利用A与A*特征值之间的关系，通过A的特征值间接推导出A*的特征值，计算量有所减少．
解法三 利用本题A的特殊情况，转换为求B的特征值，再由秩为1矩阵特征值的公式就能简捷求出A*的特征值．